cos30°をマクローリン展開で算出してみる。

あ、cos 30°はだった(^_^;)

わざわざマクローリン展開しなくても、算出できました(^◇^;)
タイトルを書いて初めて気が付きました(^_^;

とにかく、本日は、cosxを「式であらわす」とか、「分数で」とか、じゃなくて、
小数点で、実際に使える形で算出してみようと思います。

大学初年度に習ったのだけれど

「マクローリン展開」

スコットランドの数学者コリン・マクローリン（1698～1746）に由来します。

この日記で解く三角関数への応用は、マクローリンよりも早く、インドの数学者マーダヴァ（1340～1425）が計算して発表した記録があるそうです。

僕は、大学初年度の数学の授業で習った覚えがあります。

ただし、「習った。」と言う記憶があるだけで、中身をきれいサッパリ忘れていました。

ふと気になってネット検索しました。

北海道大学の先生が「高校生のため」と銘打って、

易しく教えてくれているページがヒットしました。

（大学のサーバーに移転した旨が記されていますが、一応トップページは）

josch(よっしゅ)のページ

当該「高校生のためのマクローリン展開」は、

高校生のための マクローリン展開（１）

です。

このページを参考にしながら、本日はcos 30°を算出したいと思います。

本日やること

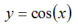
として、
xを0°から90°まで計算します。

ちなみに、0°から90°までを求めれば、

0°から360°、全ての角度についてのcosが解ります。

(90°から180°は、90°から0°までの値に-1を掛ければ良いし、180°～360°は、180°～0°と同じですので。）

 

単位円でおさらい

実際に計算を始める前に、

コサインってナンだっけ？

と言うところから、おさらいします。

半径1の円に接する直角三角形ABCで考えます。

・ 頂点Cが直角

・ 頂点Aは円の中心

・ 頂点Bは円周上

の直角三角形ABCです。

cos(x)は、

直角三角形の三つの辺のうち、

角度xの角Aと直角Cの辺ACの長さ

を

斜辺ABの長さ

で割った値です。

ここで、辺ABの長さは接する円の半径で、1です。

求めるcos(x)は、辺ACの長さです。

角度xを小さくすると、ACは徐々に長くなります。

x=0°にすると（既に三角形ではありませんが、）ACとABは一致します。

つまり、

角度xを大きくすると、ACは徐々に短くなります。

x=90°にすると、（やはり既に三角形ではありませんが）ACは0になります。

xが90°を越えると、反対側に向かって鏡が像を作るように、マイナスに増えていきます。（マイナスだから、「減っていきます。」かな？）

以上がおさらいです。

少しおさらいが長かったですね(^_^;

では、cos(x)の値を求める作業に入ります。

自分で計算する前に、表計算ソフトに正解を教えてもらう

えーっと、最初にズルをして、表計算ソフトに答えを教えてもらいます（笑）

xの単位は「°（度）」がなじみ深いと思いますが、

計算のため、180°を円周率（π）＝3.141592…に置き換えた単位を使います。

この角度の単位を「ラジアン」と言います。

ラジアンの説明は省略します。

表計算ソフトのお答えは、下記の通りです。

15°きざみで教えてもらいました。

 

とりあえず8次式に展開してみる。

では、本題です。

 

「cos(x)をxの8次式（別に8次でなくても良いのだが）であらわせないかなぁ。」

と、言うのがマクローリン展開です。

A₀～A₈の定数を決められれば、計算ができるはずです。

A₀を求める。

とりあえず、x=0を代入します。

A₀以外の項が0になります。

cos(0)は、1ですので、

です。

(!o!)オオ! 、A₀を求めることができました。＼(^-^)／

 

A₁を求める。

両辺を微分します。

再びx=0を代入します。

A₁以外の項が0になりました。

-sin(0)は、0ですので、

おぉ、A₁も求めることが出来ました。

A₂を求める。

さらに、両辺を微分します。

三度めのx=0を代入すると、

A₂以外の項が0になります。

-cos(0)は、-1ですので、

おぉ、A2も求めることができました。

A₃を求める。

調子に乗って続けます。

微分３回目。

やっぱりx=0を代入します。

A₄を求める。

微分４回目。

x=0を代入

A₅を求める。

微分５回目。

x=0を代入。

なんとなく、法則が解ってきたような気がします。

このまま同じ作業を進めます。

A₆を求める。

微分６回目。

x=0を代入

A₇を求める。

微分７回目。

x=0を代入。

A₈を求める。

微分８回目。

x=0を代入

ふぅ。

8次の近似式が完成しました。

それでは、これまでの結果をまとめます。

cos(x)を筆算するために、8次式を作りました。

この係数A₀～A₈を、以下の通り算出しました。

この係数を上の式に代入します。

係数が0の項を消します。

厳密には、8次式で満足できません。９次、10次、と永遠に続きます。

でも、見ての通り、次数が高いほど係数が小さくなります。（分母が大きくなります。）8次くらいで充分なんじゃないか、とカンが働きます。

さて、僕のカンは正しいのか、正しくないのか。

次に、実際にxに、15度、30度と数字を代入して計算してみましょう。

と、思ったけれど、長くなりました。

一旦これで日記をアップロードします。

続きはまた、後日。

つづきはこちら。

暇なのでマクローリン展開でcos30度を計算する（つづき） - daniel-yangのブログ